Theory 1

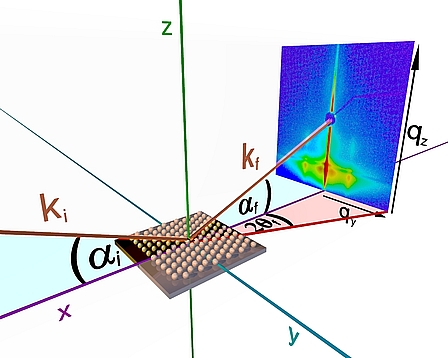
Figure 1: GISAXS geometry

The geometry of a GISAXS experiment is illustrated in Figure 1. A monochromatic x-ray beam with the wavevector ki is directed on a surface with a very small incident angle αi with respect to the surface. The Cartesian z-axis is the normal to the surface plane, the x-axis is the direction along the surface parallel to the beam and the y-axis perpendicular to it. The x-rays are scattered along kf in the direction (2θf, αf) by any type of electron density fluctuations at the illuminated portion of the surface. The appearing scattering wavevector q for the three spatial directions is defined by:

In general, a 2-D detector records the scattered intensity at angles of a few degrees for the observation of lateral sizes ranging from a few up to hundreds of nanometers. The sample detector distance is normally in a range of 1 to 4 meters for GISAXS, and up to 13 meters for grazing incidence ultra small angle scattering (GIUSAXS) experiments whereas the detectable lateral size increases to several micrometers. Gas-filled wire frame detectors, CCD-detectors as well as imaging plates are in use. The direct and the reflected specular beam are often suppressed by two small beamstops to prevent damage or saturation of the detector.

The scattering intensity I(q) for a lateral electron density fluctuation on the surface can be described as

where F is the form factor and S(q) is the total interference function. The interference function describes the spatial arrangement of the objects on the surface and thus their lateral correlations. It is the Fourier transform of the island position autocorrelation function. In the simple Born approximation (BA), F is the Fourier transform of the shape function of the objects and is defined as

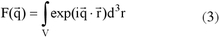
If reflection-refraction effects at the surface of the substrate have to be accounted for, F has to be calculated within the distorted wave Born approximation (DWBA) and has a more complex expression. Figure 2 illustrates the physical picture of the full calculation for the scattering cross section in the DWBA, which is given by

Figure 2: The four scattering events in the DWBA

The four terms involved are associated to different scattering events, which involve or not a reflection of either the incident beam or the final beam collected on the detector. These waves interfere coherently, giving rise to the effective form factor (FDWBA), in which the classical form factor comes into play but with respect to the specific wavevector transfers. Each term is weighted by the corresponding Fresnel reflection coefficient R, either in incidence or in reflection. The reduced reflectivity of the substrate by an uncorrelated roughness can be calculated in a classical way with a mean standard deviation. The scattered cross section is proportional to the scattered intensity and thus to the modulus square of the Fourier transform of the electron density. The polarisation effect for x-rays can be dropped out safely as the scattering angles are small. The combination of the calculated form factor within the DWBA together with the total interference function leads to the expression for the total incoherent cross section:

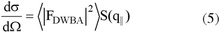
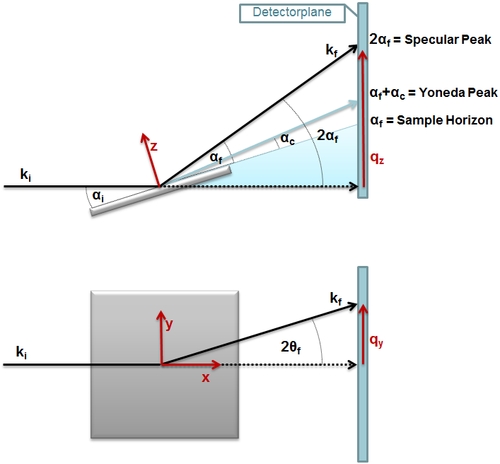
In Figure 3 the scattering situation of a GISAXS experiment is shown. This situation is only valid for very small angles αf and small qz, as the surface normal z and the detectorplane are not exactly parallel to each other. For larger angles this has taken into account. Below the sample horizon scattering is not observable. At the so called Yoneda Peak, the scattering of the material has its maximum and the qz position depends on its critical angle αc.

Figure 3: Top and side-view of a GISAXS experiment

theory page 2 >>